
DOI:10.1016/j.jmbbm.2020.103634
本文仅以单纤维的几何和弹塑性力学性能为基础,辅以膜的重量和体积的测量,预测了电纺聚丙交酯膜的三维结构和宏观力学响应,并将所得计算模型应用于电纺网络的非仿射微运动学研究。为此,从膜的扫描电子显微照片中提取描述面内纤维形态的统计参数,并通过匹配真实纤维垫的孔隙率来生成计算网络模型。将虚拟网络在结构上与计算机断层扫描进行比较,并就其宏观力学响应与单轴拉伸测试进行比较。所获得的虚拟网络结构与实际网络中的纤维配置非常吻合,对平均直径为1.10μm和0.70μm的两种膜的力学响应的严格预测定性地捕获了实验行为。但是,只有在降低单纤维测试中确定的杨氏模量,屈服应力和硬化斜率,并在纤维较细的膜模型中降低纤维间键的密度后,才能获得良好的定量一致性。模拟结果证明了研究电纺网络多尺度力学方法的有效性和优点,但也指出了网络中电纺纤维的特性与为单纤维表征而产生的性能之间的潜在差异,并突显了电纺网络中纤维之间键合密度和质量的现有不确定性。

图1.(a)样品电纺材料的阈值CT。(b)从CT数据的后处理中提取的纤维中心线。(c)从微观结构已知的数值模型中提取的纤维中心线。
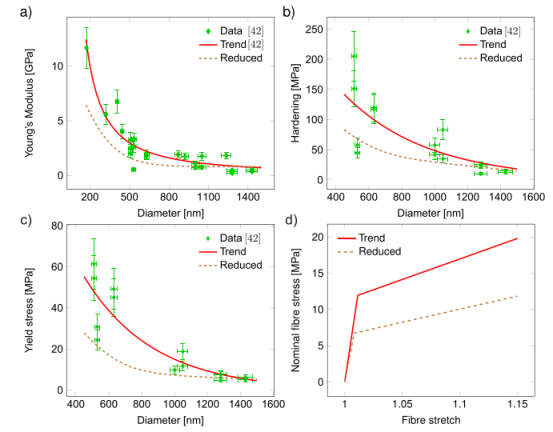
图2.取决于纤维直径的单纤维材料参数。具有合适的拟合趋势线和减小关系的(a)杨氏模量、(b)硬化和(c)屈服应力的实验数据。(c)比较具有拟合趋势的直径dF=1.10和参数减小的纤维的单纤维标称应力-拉伸曲线。
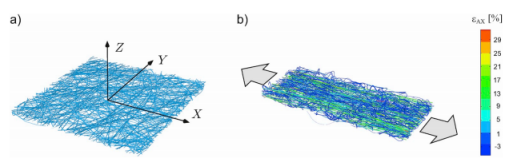
图3.单轴载荷下离散网络的有限元模拟。(a)参考配置。(b)模型对施加的纵向网络拉伸(λx=1.15)的典型响应,显示局部轴向基本应变εAX。
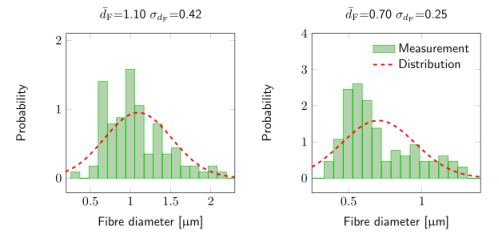
图4.(a)样品I和(b)样品II的单纤维直径和相应的高斯分布直方图。

图5.(a,b)样品I和(b,d)样品II离散模型的(a,b)SEM和(c,d)渲染图像的俯视分解图。比例尺适用于所有图像。
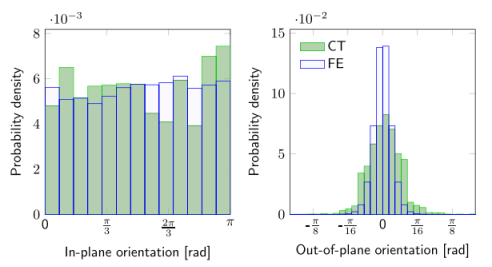
图6.从微结构信息有限元模型和电纺样品的CT中获得的面内和面外定向分布比较。
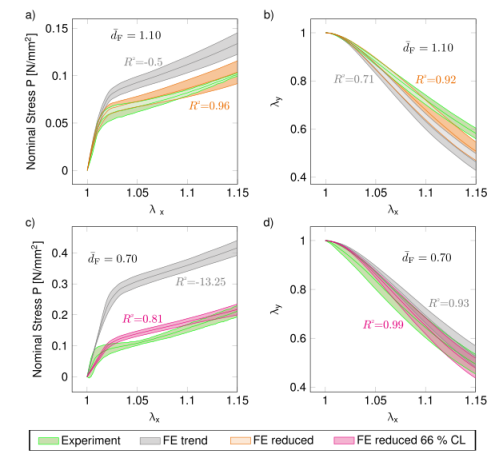
图7.(a)实验获得的样品I和(c)样品II的数值模型和通过数值模型预测的应力-拉伸曲线的比较,以及(b)样品I和(d)样品II的面内横向拉伸与纵向拉伸λy-λx曲线。所有图表分别显示N=3个数据集的平均值和标准偏差(阴影区域)。用各自的平均值评估确定系数。
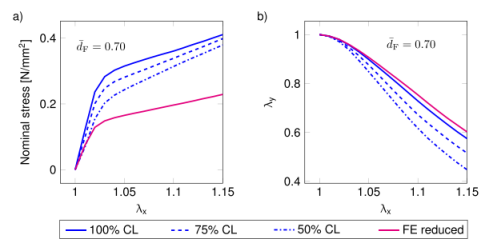
图8.(a)交联量和减少的材料参数对数值模型预测的应力-拉伸曲线的影响,以及(b)样品II的面内横向与纵向拉伸λx-λy曲线的影响。
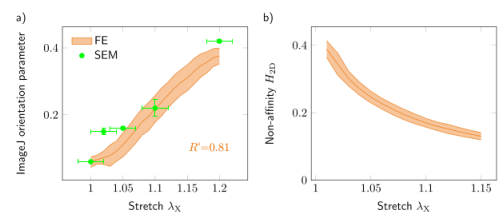
图9.(a)由ImageJ定向参数量化的纤维重新定向的比较,该参数来自后处理的俯视SEM和离散模型的渲染图像。对于SEM数据,假定网络拉伸λ1的误差为2%。(b)由参数H2D(等式(8))定量的单轴张力中的非仿射变形,该参数由具有降低单纤维性能的样品I的数据模型显示。SEM数据的ImageJ定向参数的误差以及FE数据的阴影区域分别代表N=3个数据集的标准偏差。(a)中的测定系数用各自的平均值评估。
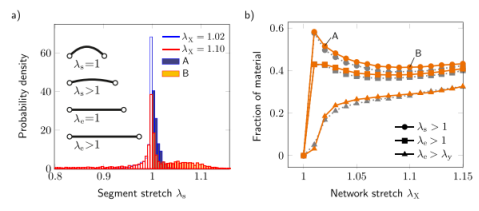
图10.(a)两个宏观网络拉伸λx的纤维拉伸分布直方图。直方图的蓝色和橙色阴影部分分别表示A:λx=1.02和B:λx=1.10的细长段(λs>1)的片段。(b)具有细长纤维段(λs,λe> 1)或段拉伸超过其屈服阈值(λe>λy)的纤维材料的片段。样品I的数值模型给出的数据具有减少的材料(橙色实线)和初步确定的(虚线灰色)性能(见图2b)。
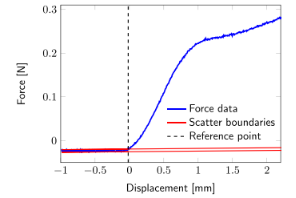
图A1.参考点算法用于力-位移数据。红线显示分散边界。黑色虚线表示定义的参考点。
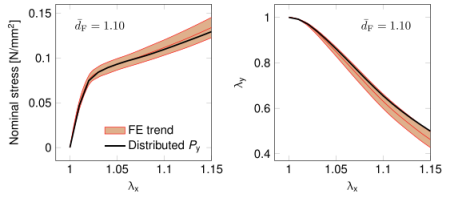
图B2.样本I的微结构离散模型对单轴张力的响应的比较(通过拟合的单纤维机械参数的平均值(FE趋势)与正态分布的单纤维屈服应力(分布式Py)进行比较)。FE趋势的值表示为平均值和标准偏差(阴影区域)。
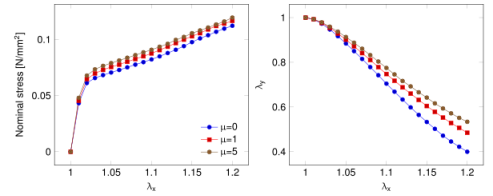
图C3.摩擦系数μ对样品I网络模型的宏观响应的影响。
